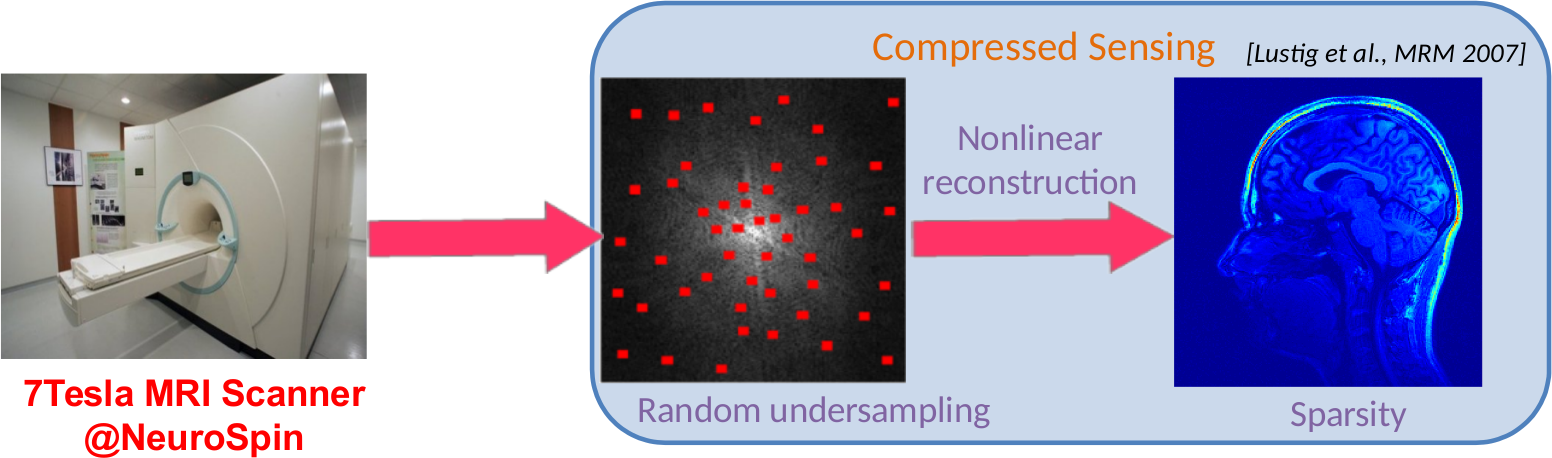
Most scientific developments rely on new acquisition systems which present improved resolution. In biomedical imaging, the advent of Magnetic Resonance Imaging (MRI) strongly impacted medicine and neuroscience while in astrophysics, gravitational waves have recently been discovered thanks to a new generation of instruments.
In COSMIC, experts in MR and astrophysical image processing have joined their efforts to work on Compressed Sensing because:
- The image formation model (or forward modeling) is very similar, i.e. the data are collected in the Fourier (spatial frequency) domain.
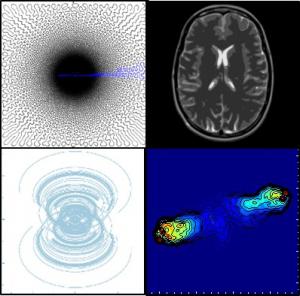
- The images are compressible in similar transform domains (e.g., wavelets), i.e. they can be well approximated by sparse decomposition in an appropriate transform domain.
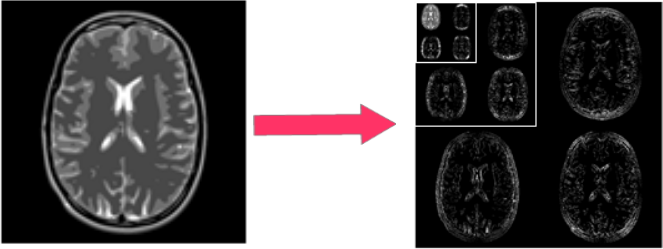
- The same convex optimization algorithms can be deployed to perform nonlinear image reconstruction in both application fields.
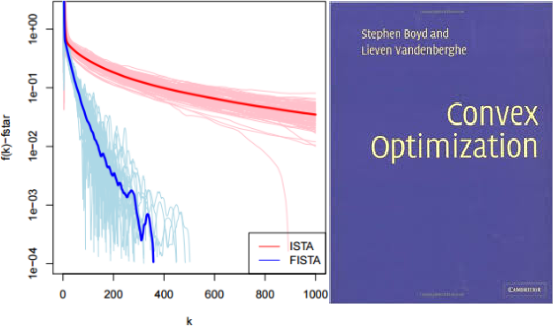
Hence, some efforts can be factorized out to push forward the limits in terms of spatial resolution or speedup acquisition in MRI.
MRI is a non-invasive and non-ionizing imaging technique that offers a variety of contrast mecahnisms, and enables excellent visualization of anatomical structures and physiological functions. However, the data in MRI, which correspond to the samples in k-space or the spatial Fourier transform of the object (e.g., brain, liver, heart ...), are collected sequentially in time along piecewise continuous or more regular traejectories. Hence, a drawback of MRI that affects both image quality and clinical throughput is that it is a relatively slow imaging technique.

MR image resolution improvement in a standard scanning time (e.g., 200μm isotropic in 15 min) would allow neuroscientists and doctors to push the limits of their current knowledge and to significantly improve both their diagnosis and patients' follow-up. This could be achieved thanks to the recent Compressed Sensing (CS) theory, which has revolutionized the way of acquiring data by overcoming the Shannon-Nyquist criterion. This breakthrough has been accomplished by combining three key
ingredients:
- (i) pseudo-random acquisitions,
- (ii) image representation using sparse decompositions (e.g., wavelets),
- (iii) nonlinear image reconstruction.
Using CS, data can be massively undersampled by a given acceleration factor “R” while ensuring conditions for optimal image recovery as illustrated below.